meandr allows for easy generation of coordinates that are random, yet continuously differentiable. This is particularly useful for simulating time-series measurements of physical phenomena that maintain a clear local trajectory.
Installation
devtools::install_github("sccmckenzie/meandr")Why meandr?
Suppose we want to simulate behavior of a “somewhat random” time-series phenomenon.
- Outdoor temperature
- Train station crowd density
- Stock price
Although we can’t predict the exact values of these examples, we know how they will behave to a certain extent. For instance, outdoor temperature is not going to drop by 100 degrees in 1 second.
We could use method #1 below:
method_1 <- data.frame(t = 1:100,
f = rnorm(100))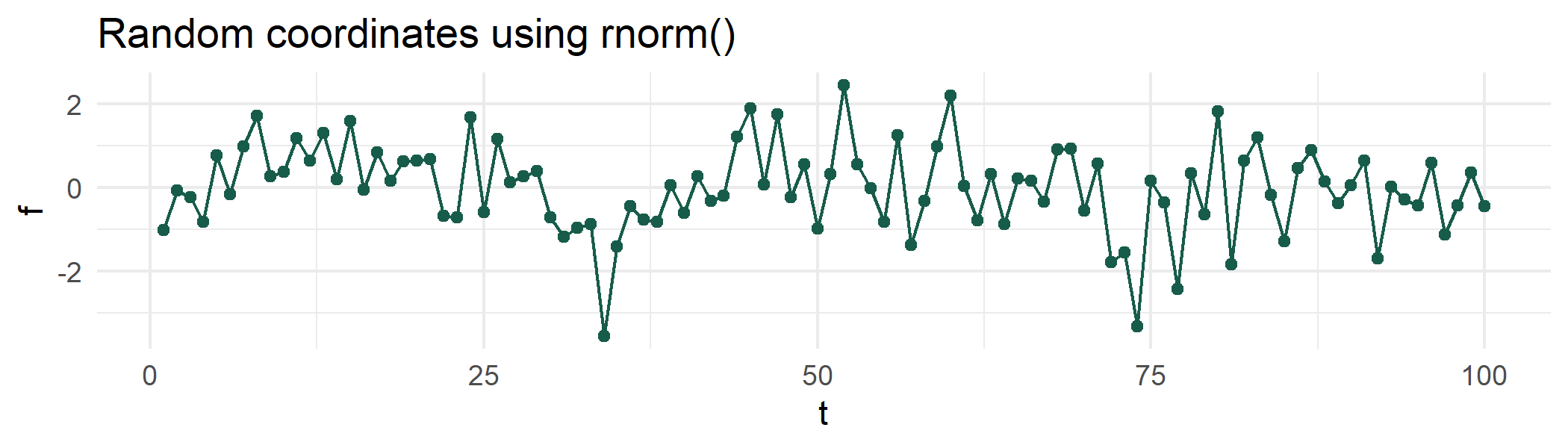
The above data doesn’t exhibit any prolonged directional consistency. This may not adequately emulate the character of the above examples.
meandr offers a solution to this problem. Each call to meandr() generates a unique tibble of t and f coordinates. For reproducibility, a seed argument is provided.
library(meandr)
df1 <- meandr(n_points = 100,
n_nodes = 20,
seed = 2)
df1
#> # A tibble: 100 x 2
#> t f
#> <dbl> <dbl>
#> 1 0.01 -0.00400
#> 2 0.02 -0.0160
#> 3 0.03 -0.0360
#> 4 0.04 -0.0640
#> 5 0.05 -0.100
#> 6 0.06 -0.144
#> 7 0.0700 -0.196
#> 8 0.08 -0.256
#> 9 0.09 -0.324
#> 10 0.10 -0.400
#> # ... with 90 more rows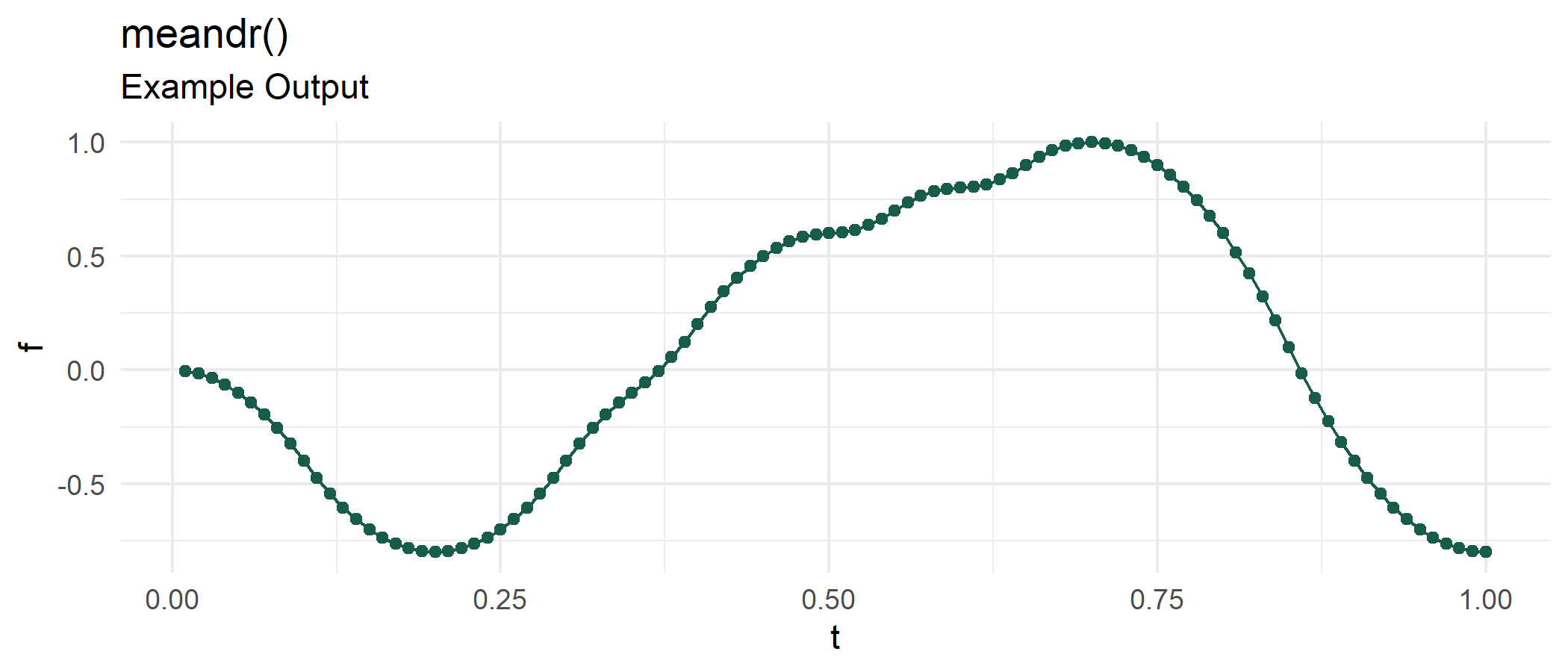
Observe df1 curve trajectory never radically changes between two points. This is a key feature of meandr: all curves are continuously differentiable.